Aquí hay un problema: Tu empresa asigna a los contratistas para cumplir los contratos. Miras tus listas y decides qué contratistas están disponibles para un contrato de un mes y revisas tus contratos disponibles para ver cuáles son para tareas de un mes de duración. Dado que sabes con qué eficacia cada contratista puede cumplir cada contrato, ¿cómo asignar a los contratistas para maximizar la eficacia general para ese mes?
Este es un ejemplo del problema de asignación, y el problema se puede resolver con el clásico algoritmo húngaro.

El algoritmo húngaro (también conocido como el algoritmo de Kuhn-Munkres) es un algoritmo de tiempo polinomico, el cual maximiza la ponderación de peso en un gráfico bipartito ponderado. Aquí, los contratistas y los contratos pueden ser modelados como un gráfico bipartito, con su efectividad como el peso de los bordes entre el contratista y los nodos de contrato.
En este artículo, aprenderás sobre una implementación del algoritmo húngaro que utiliza el algoritmo Edmonds-Karp para resolver el problema de asignación lineal. También aprenderás cómo el algoritmo de Edmonds-Karp es una ligera modificación del Ford-Fulkerson y la importancia de esta modificación.
El Problema de Flujo Máximo
El problema de flujo máximo en sí mismo se puede describir informalmente como el problema de mover algo de fluido o gas, a través de una red de tuberías desde una única fuente hasta un único terminal. Esto se hace con la suposición de que la presión en la red es suficiente para asegurar que el fluido o gas no pueda permanecer en cualquier longitud de tubería o instalación de tuberías (los lugares donde se reúnen diferentes longitudes de tubería).
Al realizar ciertos cambios en el gráfico, el problema de asignación puede convertirse en un problema de flujo máximo.
Preliminares
Las ideas necesarias para resolver estos problemas surgen en muchas disciplinas matemáticas y de ingeniería, a menudo conceptos similares son conocidos por diferentes nombres y expresados de diferentes maneras (por ejemplo, matrices de adyacencia y listas de adyacencia). Dado que estas ideas son bastante esotéricas, se hacen elecciones sobre la forma en que estos conceptos se definirán generalmente para cualquier entorno determinado.
Este artículo no asumirá ningún conocimiento previo más allá de una pequeña teoría introductoria de conjuntos.
Las implementaciones en este post representan los problemas como grafos dirigidos (dígrafo).
Digrafo
Un digrafo tiene dos atributos, setOfNodes y setOfArcs. Ambos de estos atributos son conjuntos (colecciones desordenadas). En los bloques de código en este post, estoy usando Python frozenset, pero ese detalle no es particularmente importante.
DiGraph = namedtuple('DiGraph', ['setOfNodes','setOfArcs'])
(Nota: Este y todos los demás códigos de este artículo están escritos en Python 3.6.)
Nodos
Un nodo n está compuesto de dos atributos:
x.uid != y.uid
n.datum: Esto representa cualquier objeto de datos.
Node = namedtuple('Node', ['uid','datum'])
Arco
Un arco a está compuesto de tres atributos:
-
a.fromNode: Éste es un nodo, como lo definimos arriba.
-
a.toNode: Éste es un nodo, como lo definimos arriba.
-
a.datum: Este representa cualquier objeto de data.
Arc = namedtuple('Arc', ['fromNode','toNode','datum'])
El set de arcos en el dígrafo representa una relación binaria en los nodos en el dígrafo. La existencia del arco a implica que existe una relación entre a.fromNode y a.toNode.
En un gráfico dirigido (en oposición a un gráfico no dirigido), la existencia de una relación entre a.fromNode y a.toNode no implican que una relación similar entre a.toNode y a.fromNode existe.
Esto se debe a que en un gráfico no dirigido, la relación que se expresa no es necesariamente simétrica.
DíGrafos
Nodos y arcos pueden usarse para definir un dígrafo, pero por conveniencia, en los algoritmos siguientes, se representará un dígrafo usando como un diccionario.
Aquí hay un método que puede convertir la representación gráfica anterior en una representación de diccionario similar a ésta:
def digraph_to_dict(G):
G_as_dict = dict([])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
pdg(G)
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
pdg(G)
raise KeyError(err_msg)
G_as_dict[a.fromNode] = (G_as_dict[a.fromNode].union(frozenset([a]))) if (a.fromNode in G_as_dict) else frozenset([a])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if a.toNode not in G_as_dict:
G_as_dict[a.toNode] = frozenset([])
return G_as_dict
Y aquí hay otro que lo convierte en un diccionario de diccionarios, otra operación que será útil:
def digraph_to_double_dict(G):
G_as_dict = dict([])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.fromNode not in G_as_dict):
G_as_dict[a.fromNode] = dict({a.toNode : frozenset([a])})
else:
if(a.toNode not in G_as_dict[a.fromNode]):
G_as_dict[a.fromNode][a.toNode] = frozenset([a])
else:
G_as_dict[a.fromNode][a.toNode] = G_as_dict[a.fromNode][a.toNode].union(frozenset([a]))
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if a.toNode not in G_as_dict:
G_as_dict[a.toNode] = dict({})
return G_as_dict
Cuando el artículo habla de un dígrafo como lo representa el diccionario, mencionará G_as_dict para hacerle referencia.
A veces es de ayuda tomar un nodo de un dígrafo G hasta su uid (identificador único):
def find_node_by_uid(find_uid, G):
nodes = {n for n in G.setOfNodes if n.uid == find_uid}
if(len(nodes) != 1):
err_msg = 'Node with uid {find_uid!s} is not unique.'.format(**locals())
raise KeyError(err_msg)
return nodes.pop()
Al identificar gráficos, a veces las personas usan los términos nodo y vértice para referirse al mismo concepto; esto mismo se dice de los términos arco y borde.
Hay dos representaciones gráficas in Python, ésta la cual usa diccionarios y otra la cual usa objetos para representar gráficos. La representación en este post se encuentra entre estas dos representaciones comunes.
Esta es mi representación de un dígrafo. Hay muchas como ésta, pero ésta es la mía.
Caminos y Vías
Deja que S_Arcs sea una secuencia definitiva (colección ordenada) de arcos en un dígrafo G tanto que si a es cualquier arco en S_Arcs excepto por el último, y b sigue a a en la secuencia, entonces debe haber un nodo n = a.fromNode en G.setOfNodes como a.toNode = b.fromNode.
Comenzando desde el primer arco en S_Arcs, y continuando hasta el último arco en S_Arcs, recolecta (en el orden encontrado) todos los nodos n como los definimos arriba entre cada dos arcos consecutivos en S_Arcs. Marca la colección ordenada de nodos coleccionados durante esta operación S_{Nodes}.
def path_arcs_to_nodes(s_arcs):
s_nodes = list([])
arc_it = iter(s_arcs)
step_count = 0
last = None
try:
at_end = False
last = a1 = next(arc_it)
while (not at_end):
s_nodes += [a1.fromNode]
last = a2 = next(arc_it)
step_count += 1
if(a1.toNode != a2.fromNode):
err_msg = "Error at index {step_count!s} of Arc sequence.".format(**locals())
raise ValueError(err_msg)
a1 = a2
except StopIteration as e:
at_end = True
if(last is not None):
s_nodes += [last.toNode]
return s_nodes
-
Si cualquier nodo aparece más de una vez en la secuencia
S_Nodes entonces llama a S_Arcs un Camino por dígrafo G.
-
De otro modo, llama
S_Arcs una vía de list(S_Nodes)[0] a list(S_Nodes)[-1] en el dígrafo G.
Nodo Fuente
Llama al nodo s un nodo fuente en dígrafo G si s está en G.setOfNodes y G.setOfArcs no contiene arco a como a.toNode = s.
def source_nodes(G):
to_nodes = frozenset({a.toNode for a in G.setOfArcs})
sources = G.setOfNodes.difference(to_nodes)
return sources
Nodo Terminal
Llama al nodo t un nodo terminal en el dígrafo G si t está en G.setOfNodes y G.setOfArcs no contiene arco a como a.fromNode = t.
def terminal_nodes(G):
from_nodes = frozenset({a.fromNode for a in G.setOfArcs})
terminals = G.setOfNodes.difference(from_nodes)
return terminals
Cortes y Cortes s-t
Un corte cut de un dígrafo G conectado es un subset de arcos desde G.setOfArcs el cual parte el set de nodos G.setOfNodes en G. G está conectado si cada nodo n en G.setOfNodes tiene al menos un arco a en G.setOfArcs como n = a.fromNode o n = a.toNode, pero no a.fromNode != a.toNode.
Cut = namedtuple('Cut', ['setOfCutArcs'])
La definición de arriba se refiere al subset de arcos, pero también puede definir una partición de los nodos de G.setOfNodes.
Para las funciones predecessors_of y successors_of, n es un nodo en el set G.setOfNodes de dígrafo G, y cut es un corte de G:
def cut_predecessors_of(n, cut, G):
allowed_arcs = G.setOfArcs.difference(frozenset(cut.setOfCutArcs))
predecessors = frozenset({})
previous_count = len(predecessors)
reach_fringe = frozenset({n})
keep_going = True
while( keep_going ):
reachable_from = frozenset({a.fromNode for a in allowed_arcs if (a.toNode in reach_fringe)})
reach_fringe = reachable_from
predecessors = predecessors.union(reach_fringe)
current_count = len(predecessors)
keep_going = current_count - previous_count > 0
previous_count = current_count
return predecessors
def cut_successors_of(n, cut, G):
allowed_arcs = G.setOfArcs.difference(frozenset(cut.setOfCutArcs))
successors = frozenset({})
previous_count = len(successors)
reach_fringe = frozenset({n})
keep_going = True
while( keep_going ):
reachable_from = frozenset({a.toNode for a in allowed_arcs if (a.fromNode in reach_fringe)})
reach_fringe = reachable_from
successors = successors.union(reach_fringe)
current_count = len(successors)
keep_going = current_count - previous_count > 0
previous_count = current_count
return successors
Deja que cut sea un corte del dígrafo G.
def get_first_part(cut, G):
firstPartFringe = frozenset({a.fromNode for a in cut.setOfCutArcs})
firstPart = firstPartFringe
for n in firstPart:
preds = cut_predecessors_of(n,cut,G)
firstPart = firstPart.union(preds)
return firstPart
def get_second_part(cut, G):
secondPartFringe = frozenset({a.toNode for a in cut.setOfCutArcs})
secondPart = secondPartFringe
for n in secondPart:
succs= cut_successors_of(n,cut,G)
secondPart = secondPart.union(succs)
return secondPart
cut es un corte del dígrafo G si: (get_first_part(cut, G).union(get_second_part(cut, G)) == G.setOfNodes) y (len(get_first_part(cut, G).intersect(get_second_part(cut, G))) == 0) cut es llamado un corte x-y si (x in get_first_part(cut, G)) y (y in get_second_part(cut, G) ) y (x != y). Cuando el nodo x en un corte x-y cut es un nodo fuente y el nodo y en el corte x-y es un nodo terminal, luego este corte es llamado un corte s-t.
STCut = namedtuple('STCut', ['s','t','cut'])
Redes de Flujo
Puedes usar un dígrafo G para representar una red de flujo.
Asigna cada nodo n, donde n está en G.setOfNodes un n.datum que es un FlowNodeDatum:
FlowNodeDatum = namedtuple('FlowNodeDatum', ['flowIn','flowOut'])
Asigna cada arco a, donde a es un G.setOfArcs y a.datum que es un FlowArcDatum.
FlowArcDatum = namedtuple('FlowArcDatum', ['capacity','flow'])
flowNodeDatum.flowIn y flowNodeDatum.flowOut son números realespositivos.
flowArcDatum.capacity y flowArcDatum.flow también son números reales positivos.
Por cada nodo nodo n en G.setOfNodes:
n.datum.flowIn = sum({a.datum.flow for a in G.Arcs if a.toNode == n})
n.datum.flowOut = sum({a.datum.flow for a in G.Arcs if a.fromNode == n})
El Dígrafo G ahora representa a la red de flujo.
El flujo de G se refiere al flujo a.flow para todos los arcos a en G.
Flujos Factibles
Deja que el dígrafo G represente una red de flujo.
La red de flujo representada por G tiene flujos factibles si:
-
Por cada nodo
n en G.setOfNodes excepto por nodos fuentes y nodos terminal: n.datum.flowIn = n.datum.flowOut.
-
Por cada arco
a in G.setOfNodes: a.datum.capacity <= a.datum.flow.
La Condición 1 es llamada contención de conservación.
La Condición 2 es llamada contención de capacidad.
Capacidad de Corte
La capacidad de corte de un corte s-t stCut con un nodo fuente s y un nodo terminal t de una red de flujo representada por un dígrafo G es:
def cut_capacity(stCut, G):
part_1 = get_first_part(stCut.cut,G)
part_2 = get_second_part(stCut.cut,G)
s_part = part_1 if stCut.s in part_1 else part_2
t_part = part_1 if stCut.t in part_1 else part_2
cut_capacity = sum({a.datum.capacity for a in stCut.cut.setOfCutArcs if ( (a.fromNode in s_part) and (a.toNode in t_part) )})
return cut_capacity
Corte de Capacidad Mínima
Deja que stCut = stCut(s,t,cut) sea un corte s-t de una red de flujo representada por un dígrafo G.
stCut es el corte de capacidad mínima de la red de flujo representada por G si no hay otro corte s-t stCutCompetitor en esta red de flujo como:
cut_capacity(stCut, G) < cut_capacity(stCutCompetitor, G)
Despojando los Flujos
Me gustaría referirme al dígrafo que sería el resultado de tomar un dígrafo G y borrar todos los datos de flujo de todos los nodos en G.setOfNodes y también todos los arcos en G.setOfArcs.
def strip_flows(G):
new_nodes= frozenset( (Node(n.uid, FlowNodeDatum(0.0,0.0)) for n in G.setOfNodes) )
new_arcs = frozenset([])
for a in G.setOfArcs:
new_fromNode = Node(a.fromNode.uid, FlowNodeDatum(0.0,0.0))
new_toNode = Node(a.toNode.uid, FlowNodeDatum(0.0,0.0))
new_arc = Arc(new_fromNode, new_toNode, FlowArcDatum(a.datum.capacity, 0.0))
new_arcs = new_arcs.union(frozenset([new_arc]))
return DiGraph(new_nodes, new_arcs)
Problema de Flujo Máximo
Una red de flujo representada como un dígrafo G, un nodo fuente s en G.setOfNodes y un nodo terminal t en G.setOfNodes, G puede representar un problema de flujo máximo si:
(len(list(source_nodes(G))) == 1) and (next(iter(source_nodes(G))) == s) and (len(list(terminal_nodes(G))) == 1) and (next(iter(terminal_nodes(G))) == t)
Marca esta representación:
MaxFlowProblemState = namedtuple('MaxFlowProblemState', ['G','sourceNodeUid','terminalNodeUid','maxFlowProblemStateUid'])
Donde sourceNodeUid = s.uid, terminalNodeUid = t.uid, y maxFlowProblemStateUid es un identificador para la instancia del problema.
Solución de Flujo Máximo
Deja que maxFlowProblem represente un problema de flujo máximo. La solución al problema maxFlowProblem puede ser representado por una red de flujo representada como un dígrafo H.
El Dígrafo H es una solución factible para el problema de flujo máximo en la entrada python maxFlowProblem si:
-
strip_flows(maxFlowProblem.G) == strip_flows(H).
-
H es una red de flujo y tiene flujos factibles.
Si en adición a 1 y 2:
- No puede haber otra red de flujo representada por el dígrafo
K como strip_flows(G) == strip_flows(K) y find_node_by_uid(t.uid,G).flowIn < find_node_by_uid(t.uid,K).flowIn.
Entonces H también es una solución óptima para maxFlowProblem.
En otras palabras, una solución de flujo máximo factible puede representarse con un dígrafo, que:
-
Es idéntico al dígrafo
G del correspondiente problema de flujo máximo con la excepción del flujo n.datum.flowIn, n.datum.flowOut y el flujo a.datum.flow de cualquiera de los nodos y arcos pueden ser diferentes.
-
Representa una red de flujo que tiene flujos factibles.
Y, puede representar una solución óptima de flujo máximo si adicionalmente:
- El
flowIn para el nodo que corresponde al nodo terminal en el problema de flujo máximo es lo más grande posible (cuando las condiciones 1 y 2 siguen estando satisfechas).
Si dígrafo H representa una solución de flujo máximo : find_node_by_uid(s.uid,H).flowOut = find_node_by_uid(t.uid,H).flowIn this follows from the flujo máximo, teorema del corte mínimo (tratado abajo). Informalmente, dado que se supone que H tiene flujos viables esto significa que el flujo no puede ser ‘creado’ (con excepción del nodo fuente s) nor ‘destruído’ (con la excepción del nodo terminal t) al cruzarse con cualquier (otro) nodo (constricciones de conservación).
Dado que un problema de flujo máximo contiene sólo un nodo fuente s y un único nodo terminal t, todo flujo ‘creado’ en s debe ser ‘destruido’ en t o la red de flujo no tiene flujos factibles (la constricción de conservación hubiese sido violada).
Deja que el dígrafo H represente una solución de flujo máximo factible; el valor anterior se llama Valor de Flujo s-t de H.
Permite:
mfps=MaxFlowProblemState(H, maxFlowProblem.sourceNodeUid, maxFlowProblem.terminalNodeUid, maxFlowProblem.maxFlowProblemStateUid)
Esto significa que mfps es un estado sucesor de maxFlowProblem, lo que significa que mfps es exactamente como maxFlowProblem con la excepción de que los valores de a.flow para los arcos a en maxFlowProblem.setOfArcs puede ser diferente de a.flow para los arcos a en mfps.setOfArcs.
def get_mfps_flow(mfps):
flow_from_s = find_node_by_uid(mfps.sourceNodeUid,mfps.G).datum.flowOut
flow_to_t = find_node_by_uid(mfps.terminalNodeUid,mfps.G).datum.flowIn
if( (flow_to_t - flow_from_s) > 0):
raise Exception('Infeasible s-t flow')
return flow_to_t
Esta es una visualización de un mfps junto con su maxFlowProb asociado. Cada arco a en la imagen tiene una etiqueta, estas etiquetas son a.datum.flowFrom/a.datum.flowTo, cada nodo n en la imagen tiene una etiqueta y estas etiquetas son n.uid {n.datum.flowIn / a.datum.flowOut}.
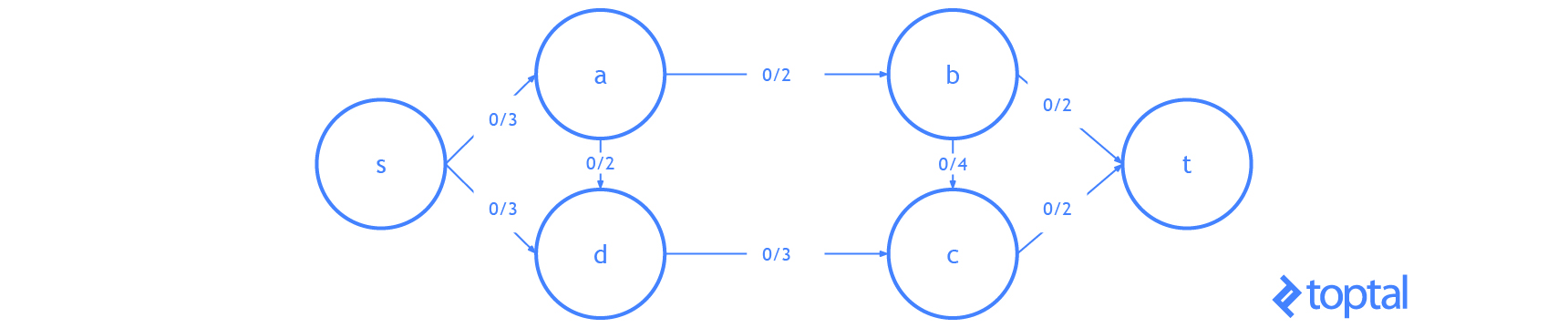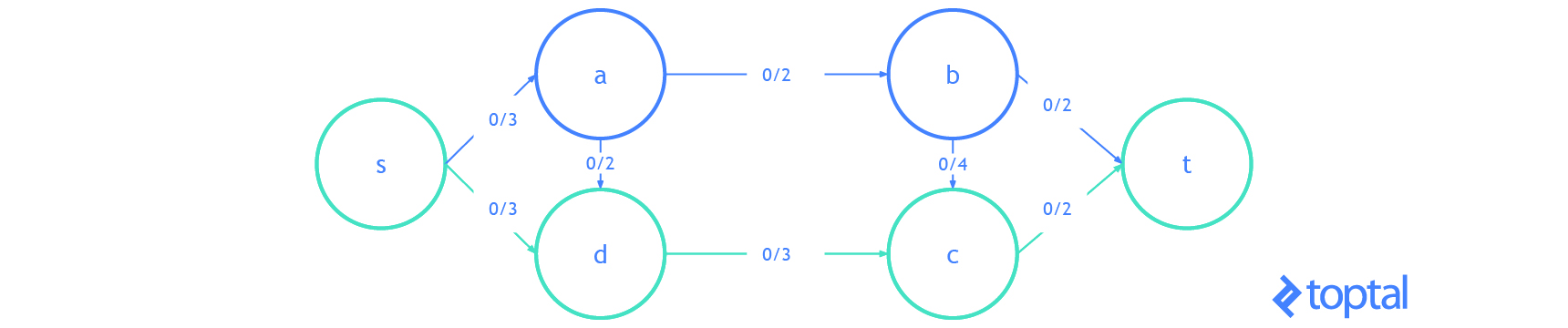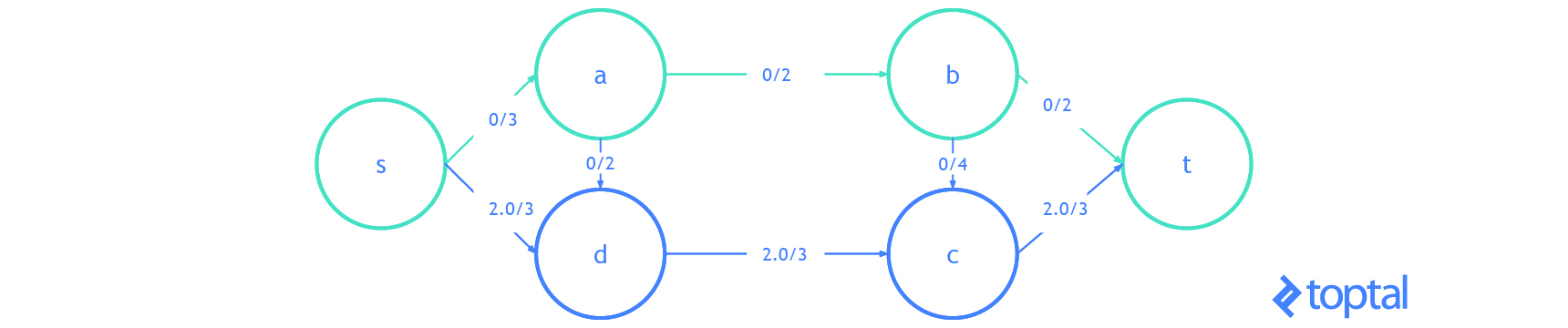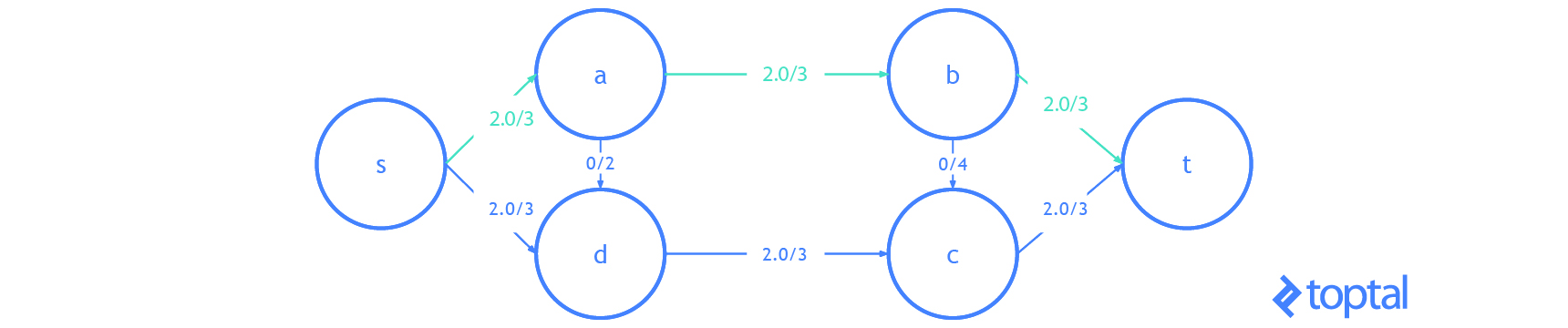
Flujo de Corte
Deja que mfps represente un estado de problema MaxFlowProblemState y deja que stCut represente un corte de mfps.G. El flujo de corte stCut está definido así:
def get_stcut_flow(stCut,mfps):
s = find_node_by_uid(mfps.sourceNodeUid, mfps.G)
t = find_node_by_uid(mfps.terminalNodeUid, mfps.G)
part_1 = get_first_part(stCut.cut,mfps.G)
part_2 = get_second_part(stCut.cut,mfps.G)
s_part = part_1 if s in part_1 else part_2
t_part = part_1 if t in part_1 else part_2
s_t_sum = sum(a.datum.flow for a in mfps.G.setOfArcs if (a in stCut.cut.setOfCutArcs) and (a.fromNode in s_part) )
t_s_sum = sum(a.datum.flow for a in mfps.G.setOfArcs if (a in stCut.cut.setOfCutArcs) and (a.fromNode in t_part) )
cut_flow = s_t_sum - t_s_sum
return cut_flow
corte de flujo s-t es la suma de los flujos de la partición que contiene el nodo fuente para la partición que contiene el nodo terminal menos la suma de los flujos de la partición que contiene el nodo terminal para la partición que contiene el nodo fuente.
Flujo Máximo, Corte Mínimo
Que maxFlowProblem represente un problema de flujo máximo y que la solución a maxFlowProblem sea representada por una red de flujo representada como dígrafo H.
Sea minStCut el corte de capacidad mínimo de la red de flujo representado por maxFlowProblem.G.
Debido a que en el flujo de flujo máximo el flujo se origina en un solo nodo fuente y termina en un único nodo terminal y, debido a las restricciones de capacidad y las restricciones de conservación, sabemos que todo el flujo que entra a maxFlowProblem.terminalNodeUid debe cruzar cualquier corte s-t, en particular debe cruzar minStCut. Esto significa:
get_flow_value(H, maxFlowProblem) <= cut_capacity(minStCut, maxFlowProblem.G)
Solución del Problema de Flujo Máximo
La idea básica para resolver un problema de flujo máximo maxFlowProblem es comenzar con una solución de flujo máximo representada por dígrafo H. Tal punto de partida puede ser H = strip_flows(maxFlowProblem.G).
The task is then to use H and by some greedyla modificación de los valores a.datum.flow de algunos arcos a en H.setOfArcs para producir otra solución de flujo máximo representada por dígrafo K de modo que K no puede todavía representar una red de flujo con flujos viables y get_flow_value(H, maxFlowProblem) < get_flow_value(K, maxFlowProblem). Mientras este proceso continúe, la calidad (get_flow_value(K, maxFlowProblem)) de la solución de flujo máximo (K) encontrada, recientemente, es mejor que cualquier otra solución de flujo máximo que se haya encontrado. Si el proceso llega a un punto en el que sabe que ninguna otra mejora es posible, el proceso puede terminar y devolverá la solución de flujo máximo óptimo.
La descripción anterior es general y omite muchas pruebas tales como, si tal proceso es posible o cuánto tiempo puede tomar, voy a dar algunos detalles más y el algoritmo.
El Teorema de Flujo Máximo, Corte Mínimo
Del libro Flows in Networks de Ford y Fulkerson, la declaración del Teorema de Flujo Máximo, Corte Mínimo (Theorem 5.1) es:
Para cualquier red, el valor de flujo máximo de s a t es igual a la capacidad de corte mínima de todos los cortes que separan s y t.
Utilizando las definiciones en este post, que se traduce en:
La solución a un maxFlowProblem representado por una red de flujo representada como dígrafo H es óptima si:
get_flow_value(H, maxFlowProblem) == cut_capacity(minStCut, maxFlowProblem.G)
Me gusta esta prueba del teorema y Wikipedia tiene otro.
El el teorema de flujo máximo, corte mínimo se utiliza para demostrar la corrección y la integridad del método de Ford-Fulkerson.
También daré una prueba del teorema en la sección después de vías de aumento.
El Método de Ford-Fulkerson y el Algoritmo de Edmonds-Karp
CLRS define el método Ford-Fulkerson (sección 26.2) así:
FORD-FULKERSON-METHOD(G, s, t):
initialize flow f to 0
while there exists an augmenting path p in the residual graph G_f augment flow f along
Gráfico Residual
El Gráfico Residual
de una red de flujo representada como el dígrafo “G” puede representarse como un dígrafo G_f:
ResidualDatum = namedtuple('ResidualDatum', ['residualCapacity','action'])
def agg_n_to_u_cap(n,u,G_as_dict):
arcs_out = G_as_dict[n]
return sum([a.datum.capacity for a in arcs_out if( (a.fromNode == n) and (a.toNode == u) ) ])
def agg_n_to_u_flow(n,u,G_as_dict):
arcs_out = G_as_dict[n]
return sum([a.datum.flow for a in arcs_out if( (a.fromNode == n) and (a.toNode == u) ) ])
def get_residual_graph_of(G):
G_as_dict = digraph_to_dict(G)
residual_nodes = G.setOfNodes
residual_arcs = frozenset([])
for n in G_as_dict:
arcs_from = G_as_dict[n]
nodes_to = frozenset([find_node_by_uid(a.toNode.uid,G) for a in arcs_from])
for u in nodes_to:
n_to_u_cap_sum = agg_n_to_u_cap(n,u,G_as_dict)
n_to_u_flow_sum = agg_n_to_u_flow(n,u,G_as_dict)
if(n_to_u_cap_sum > n_to_u_flow_sum):
flow = round(n_to_u_cap_sum - n_to_u_flow_sum, TOL)
residual_arcs = residual_arcs.union( frozenset([Arc(n,u,datum=ResidualDatum(flow, 'push'))]) )
if(n_to_u_flow_sum > 0.0):
flow = round(n_to_u_flow_sum, TOL)
residual_arcs = residual_arcs.union( frozenset([Arc(u,n,datum=ResidualDatum(flow, 'pull'))]) )
return DiGraph(residual_nodes, residual_arcs)
-
agg_n_to_u_cap(n,u,G_as_dict) regresan a la suma de a.datum.capacity para los arcos en el subset de G.setOfArcs donde el arco a está en el subset si a.fromNode = n y a.toNode = u.
-
agg_n_to_u_cap(n,u,G_as_dict) regresa la suma de a.datum.flow para todos los arcos en el subset de G.setOfArcs donde el arco a está en el subset si a.fromNode = n y a.toNode = u.
En resumen, el gráfico residual G_f representa ciertas acciones que se pueden realizar en el dígrafo ` G`.
Cada par de nodos n, u en G.setOfNodes de la red de flujo representada por dígrafo G puede generar 0,1 o 2 arcos en el gráfico residual G_f de ‘G`.
-
El par
n, u no genera arcos en G_f si no hay arco a en G.setOfArcs tal como a.fromNode = n y a.toNode = u.
-
El par
n, u genera el arco a en G_f.setOfArcs donde a representa un arco etiquetado como un flujo de impulso desde n a u a = Arco (n, u, datum = ResidualNode (n_to_u_cap_sum - n_to_u_flow_sum)) si n_to_u_cap_sum> n_to_u_flow_sum.
-
El par
n, u genera el arco a en G_f.setOfArcs donde a representa un arco etiquetado como un pull stream arc de n a u a = Arco (n, u, datum = ResidualNode (n_to_u_cap_sum - n_to_u_flow_sum)) si n_to_u_flow_sum> 0.0.
-
Cada push flow arc en
G_f.setOfArcs representa la acción de añadir un total de flujo x <= n_to_u_cap_sum - n_to_u_flow_sum a arcos en el subconjunto de G.setOfArcs donde el arc a está en el subconjunto si a.fromNode = n y a.toNode = u.
-
Cada arco de flujo de tracción en
G_f.setOfArcs representa la acción de sustraer un total de flujo x <= n_to_u_flow_sum a arcos en el subconjunto de G.setOfArcs donde arco a está en el subconjunto si a.fromNode = n y a.toNode = u.
Realizar una acción individual como empuja o hala desde G_f en los arcos aplicables en G podría generar una red de flujo sin flujos factibles porque las constricciones de capacidad o constricciones de conservación podrían ser violado en la red de flujo generada.
He aquí una visualización del gráfico residual del ejemplo anterior de visualización de una solución de flujo máximo, en la visualización cada arco a representa a.residualCapacity.

Vía en Aumento
Deja que maxFlowProblem sea un problema de flujo máximo, y deja que G_f = get_residual_graph_of (G) sea el gráfico residual de maxFlowProblem.G.
Una vía en aumento augmentingPath para maxFlowProblem es cualquier vía desde find_node_by_uid(maxFlowProblem.sourceNode,G_f) a find_node_by_uid(maxFlowProblem.terminalNode,G_f).
Resulta que una ruta de aumento augmentingPath se puede aplicar a una solución de flujo máximo representada por el dígrafo H generando otra solución de flujo máximo representada por el dígrafo K donde get_flow_value (H, maxFlowProblem) <valor de get_flow (K, maxFlowProblem) si H no es óptimo.
Aquí ves como:
def augment(augmentingPath, H):
augmentingPath = list(augmentingPath)
H_as_dict = digraph_to_dict(H)
new_nodes = frozenset({})
new_arcs = frozenset({})
visited_nodes = frozenset({})
visited_arcs = frozenset({})
bottleneck_residualCapacity = min( augmentingPath, key=lambda a: a.datum.residualCapacity ).datum.residualCapacity
for x in augmentingPath:
from_node_uid = x.fromNode.uid if x.datum.action == 'push' else x.toNode.uid
to_node_uid = x.toNode.uid if x.datum.action == 'push' else x.fromNode.uid
from_node = find_node_by_uid( from_node_uid, H )
to_node = find_node_by_uid( to_node_uid, H )
load = bottleneck_residualCapacity if x.datum.action == 'push' else -bottleneck_residualCapacity
for a in H_as_dict[from_node]:
if(a.toNode == to_node):
test_sum = a.datum.flow + load
new_flow = a.datum.flow
new_from_node_flow_out = a.fromNode.datum.flowOut
new_to_node_flow_in = a.toNode.datum.flowIn
new_from_look = {n for n in new_nodes if (n.uid == a.fromNode.uid)}
new_to_look = {n for n in new_nodes if (n.uid == a.toNode.uid) }
prev_from_node = new_from_look.pop() if (len(new_from_look)>0) else a.fromNode
prev_to_node = new_to_look.pop() if (len(new_to_look)>0) else a.toNode
new_nodes = new_nodes.difference(frozenset({prev_from_node}))
new_nodes = new_nodes.difference(frozenset({prev_to_node}))
if(test_sum > a.datum.capacity):
new_flow = a.datum.capacity
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow + a.datum.capacity
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow + a.datum.capacity
load = test_sum - a.datum.capacity
elif(test_sum < 0.0):
new_flow = 0.0
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow
load = test_sum
else:
new_flow = test_sum
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow + new_flow
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow + new_flow
load = 0.0
new_from_node_flow_out = round(new_from_node_flow_out, TOL)
new_to_node_flow_in = round(new_to_node_flow_in, TOL)
new_flow = round(new_flow, TOL)
new_from_node = Node(prev_from_node.uid, FlowNodeDatum(prev_from_node.datum.flowIn, new_from_node_flow_out))
new_to_node = Node(prev_to_node.uid, FlowNodeDatum(new_to_node_flow_in, prev_to_node.datum.flowOut))
new_arc = Arc(new_from_node, new_to_node, FlowArcDatum(a.datum.capacity, new_flow))
visited_nodes = visited_nodes.union(frozenset({a.fromNode,a.toNode}))
visited_arcs = visited_arcs.union(frozenset({a}))
new_nodes = new_nodes.union(frozenset({new_from_node, new_to_node}))
new_arcs = new_arcs.union(frozenset({new_arc}))
not_visited_nodes = H.setOfNodes.difference(visited_nodes)
not_visited_arcs = H.setOfArcs.difference(visited_arcs)
full_new_nodes = new_nodes.union(not_visited_nodes)
full_new_arcs = new_arcs.union(not_visited_arcs)
G = DiGraph(full_new_nodes, full_new_arcs)
full_new_arcs_update = frozenset([])
for a in full_new_arcs:
new_from_node = a.fromNode
new_to_node = a.toNode
new_from_node = find_node_by_uid( a.fromNode.uid, G )
new_to_node = find_node_by_uid( a.toNode.uid, G )
full_new_arcs_update = full_new_arcs_update.union( {Arc(new_from_node, new_to_node, FlowArcDatum(a.datum.capacity, a.datum.flow))} )
G = DiGraph(full_new_nodes, full_new_arcs_update)
return G
En lo anterior, TOL es un valor de tolerancia para redondear
los valores de flujo en la red. Esto es para evitar la cascada de imprecisión de los cálculos de punto flotante. Así, por ejemplo, usé ‘TOL = 10` para redondear a 10 dígitos significativos.
Deja K = augment (augmentingPath, H), entonces K representa una solución de flujo máximo factible para maxFlowProblem. Para que la afirmación sea verdadera, la red de flujo representada por K debe tener flujos factibles (no violar la restricción de capacidad o la restricción de conservación.
Aquí está el por qué: En el método anterior, cada nodo añadido a la nueva red de flujo representado por dígrafo K es una copia exacta de un nodo de dígrafo H o un nodo n que ha tenido el mismo número añadido a su n.datum.flowIn como su n.datum.flowOut. Esto significa que la restricción de conservación se cumple en “K” siempre que se cumpla en “H”. La restricción de conservación se satisface porque comprobamos explícitamente que cualquier arco nuevo a en la red tiene a.datum.flow <= a.datum.capacity; por lo tanto, siempre y cuando los arcos del conjunto H.setOfArcs que fueron copiados sin modificar en K.setOfArcs no violen la restricción de capacidad, entonces K no viola la restricción de capacidad.
También es cierto que get_flow_value (H, maxFlowProblem) <get_flow_value (K, maxFlowProblem) si H no es óptimo.
Aquí está el porqué: Para un aumento de ruta augmentingPath existe en el dígrafo la representación del gráfico residual G_f de un problema de flujo máximo maxFlowProblem entonces el último arco a en augmentingPath debe ser un arco ‘push’ y debe tener a.toNode == maxFlowProblem.terminalNode. Una ruta de aumento se define como una que termina en el nodo terminal del problema de flujo máximo para el cual es una ruta de aumento. De la definición del gráfico residual, está claro que el último arco en una vía de aumento en ese gráfico residual debe ser un arco “push” porque cualquier arco “pull” b en la vía de aumento tendrá b.toNode == maxFlowProblem.terminalNode y b.fromNode! = maxFlowProblem.terminalNode desde la definición de vía. Además, a partir de la definición de vía, está claro que el nodo terminal sólo se modifica una vez con el método augment. Así augment modifica maxFlowProblem.terminalNode.flowIn exactamente una vez y aumenta el valor de maxFlowProblem.terminalNode.flowIn porque el último arco en augmentingPath debe ser el arco que causa la modificación en maxFlowProblem.terminalNode.flowIn durante augment. Desde la definición de augment, ya que se aplica a arcos ‘push’, el maxFlowProblem.terminalNode.flowIn sólo se puede aumentar, no disminuir.
Algunas Pruebas de Sedgewick y Wayne
El libro Algorithms, cuarta edición de Robert Sedgewich y Kevin Wayne tiene algunas pruebas maravillosas y cortas (páginas 892-894) que serán útiles. Los recrearé aquí, aunque utilizaré el lenguaje que se ajuste a las definiciones anteriores. Mis etiquetas para las pruebas son las mismas que en el libro de Sedgewick.
Propuesta E: Para cualquier dígrafo H que representa una solución de flujo máximo factible a un problema de flujo máximo maxFlowProblem, para cualquier stCut get_stcut_flow(stCut,H,maxFlowProblem) = get_flow_value(H, maxFlowProblem).
Prueba: Deja stCut=stCut(maxFlowProblem.sourceNode,maxFlowProblem.terminalNode,set([a for a in H.setOfArcs if a.toNode == maxFlowProblem.terminalNode])). Proposición E se mantiene por stCut directamente desde la definición de valor de flujo s-t. Supongamos que allí deseamos mover un nodo n desde la partición s (get_first_part(stCut.cut, G)) y en la partición (get_second_part(stCut.cut, G)), para hacer esto necesitamos cambiar stCut.cut, lo cual podría cambiar stcut_flow = get_stcut_flow(stCut,H,maxFlowProblem) e invalidar proposition E. Sin embargo, veamos cómo el valor de stcut_flow cambiará a medida que hagamos este cambio. El nodo n está en equilibrio, lo que significa que la suma de flujo en nodo n es igual a la suma de flujo de ésta (esto es necesario para que H represente una solución factible).
Nota que todo el flujo que es parte de stcut_flow entrando en node n entra en él desde la partición s (el flujo entrando a node n desde la partición t que lo hace directa o indirectamentefrom no habría sido contado en el valor stcut_flow porque está yendo en la dirección errónea basándonos en la definición). Observa que todo el flujo que es parte del stcut_flow que entra al nodo n lo introduce desde la partición s (el flujo que entra al nodo n desde la partición t directa o indirectamente no se han contado en el valor stcut_flow porque está dirigiendo la dirección incorrecta basada en la definición).
Además, todo el flujo que sale n eventualmente fluirá (directa o indirectamente) hacia el nodo terminal (demostrado anteriormente). Cuando movemos el nodo n en la partición t, todo el flujo que entra n desde la partición s debe ser añadido al nuevo valor stcut_flow; sin embargo, todo el flujo que sale n debe ser restado del nuevo valor stcut_flow; la parte del flujo que se dirige directamente a la partición t se resta, ya que este flujo es ahora interno a la nueva partición t y no se cuenta como stcut_flow.
La parte del flujo desde la posición n en nodos de la partición s también debe ser restada de stcut_flow: Después de que n se mueva hacia la partición t, estos flujos serán dirigidos desde la posición partición t y en la partición s y por lo tanto no se debe tener en cuenta en el stcut_flow, ya que estos flujos eliminan la entrada en la partición s y debe ser reducido por la suma de estos flujos, y el flujo de salida de la partición s en la partición-t (donde todos los flujos de st deben terminar) debe ser reducido en la misma cantidad. Como el nodo n estaba en equilibrio antes del proceso, la actualización habrá agregado el mismo valor al nuevo valor stcut_flow al restarse, dejando la proposición E clara después de la actualización. La validez de la proposición E luego se sigue en la inducción sobre el tamaño de la partición t.
Aquí hay algunos ejemplos de redes de flujo para ayudar a visualizar los casos menos obvios donde la propuesta E se mantiene; en la imagen, las áreas rojas indican la partición s, las áreas azules representan la partición t, y los arcos verdes indican un corte s-t **. En la segunda imagen, el flujo entre **nodo A y nodo B aumenta mientras que el flujo en nodo terminal t no cambia.


Corolario: Ningún valor de flujo de corte s-t puede exceder la capacidad de corte s-t.
Proposición F. (teorema de flujo máximo y corte mínimo): Deja que f sea un flujo s-t. Las siguientes 3 condiciones son equivalentes:
-
Existe un corte s-t cuya capacidad es igual al valor del flujo
f.
-
f es un flujo máximo.
-
No hay vía de aumento con respecto a
f.
La condición 1 implica la condición 2 por el corolario. La condición 2 implica la condición 3 porque la existencia de una trayectoria aumentadora implica la existencia de un flujo con valores mayores, contradiciendo la máxima de “f”. La condición 3 implica la condición 1: Sea C_s el conjunto de todos los nodos que se pueden alcanzar desde s con un aumento de ruta en el gráfico residual. Sea C_t los arcos restantes, entonces t debe estar en C_t (según nuestra suposición). Los arcos que cruzan de C_s a C_t forman entonces un corte s-t que contiene solamente arcos a donde a.datum.capacity = a.datum.flow o a.datum.flow = 0.0. De no ser así, los nodos conectados por un arco con la capacidad residual restante a C_s estarían en el conjunto C_s ya que entonces habría un aumento de vía desde s a un nodo. El caudal a través del corte de s-t es igual a la capacidad de corte de s-t (ya que los arcos de C_s a C_t tienen caudal igual a la capacidad) y también al valor de la flujo s-t (por proposición E).
Esta afirmación del teorema de flujo máximo, min corte implica la declaración anterior de Flows in Networks.
Corolario (propiedad de integralidad): Cuando las capacidades son enteras, existe un flujo máximo de valor entero, y el algoritmo Ford-Fulkerson lo encuentra.
Prueba: Cada vía de aumento incrementa el flujo por un entero positivo, el mínimo de las capacidades no utilizadas en los arcos de empuje y los flujos en los arcos de tracción, todos los cuales son siempre enteros positivos.
Esto justifica la descripción del método Ford-Fulkerson de CLRS. El método consiste en seguir encontrando incrementando rutas y aplicando augment a la última maxFlowSolution encontrando mejores soluciones, hasta no más incrementando ruta, lo que significa que la última solución de flujo máximo es óptimo.
De Ford-Fulkerson a Edmonds-Karp
Las preguntas restantes con respecto a la resolución de problemas de flujo máximo son:
-
¿Cómo deben construirse caminos de aumento?
-
¿Terminará el método si usamos números reales y no números enteros?
-
¿Cuánto tiempo tomará terminar (si lo hace)?
El algoritmo Edmonds-Karp especifica que cada ruta de aumento se construye mediante una búsqueda de amplitud (BFS) del gráfico residual; resulta que esta decisión del punto 1 también obligará al algoritmo a terminar (punto 2) y permite que el tiempo asintótico y la complejidad del espacio a ser determinados.
Primero, aquí hay una implementación BFS:
def bfs(sourceNode, terminalNode, G_f):
G_f_as_dict = digraph_to_dict(G_f)
parent_arcs = dict([])
visited = frozenset([])
deq = deque([sourceNode])
while len(deq) > 0:
curr = deq.popleft()
if curr == terminalNode:
break
for a in G_f_as_dict.get(curr):
if (a.toNode not in visited):
visited = visited.union(frozenset([a.toNode]))
parent_arcs[a.toNode] = a
deq.extend([a.toNode])
path = list([])
curr = terminalNode
while(curr != sourceNode):
if (curr not in parent_arcs):
err_msg = 'No augmenting path from {} to {}.'.format(sourceNode.uid, terminalNode.uid)
raise StopIteration(err_msg)
path.extend([parent_arcs[curr]])
curr = parent_arcs[curr].fromNode
path.reverse()
test = deque([path[0].fromNode])
for a in path:
if(test[-1] != a.fromNode):
err_msg = 'Bad path: {}'.format(path)
raise ValueError(err_msg)
test.extend([a.toNode])
return path
Utilicé un deque del módulo de colecciones de python.
Para responder a la pregunta 2, voy a parafrasear otra prueba de Sedgewick y Wayne: Proposición G. El número de caminos de incremento necesarios en el algoritmo Edmonds-Karp con nodos N y arcos es como máximo NA/2. Prueba: Cada ruta de aumento tiene un arco de cuello arco - un arco que se suprime del gráfico residual porque corresponde bien a un arco de empuje que se llena a capacidad o un arco de tracción a través del cual el flujo se convierte en 0. Cada vez que un arco se convierte en un cuello de botella arco, la longitud de cualquier trayecto de aumento a través de él debe aumentar en un factor de 2. Esto es porque cada nodo en una ruta puede aparecer sólo una vez o no en absoluto (de la definición de ruta) ya que las rutas se están explorando desde la más corta ruta a lo más largo que significa que por lo menos un nodo más debe ser visitado por la siguiente ruta que atraviesa el cuello de botella nodo que significa un adicional de 2 arcos en el camino antes de llegar en el nodo. Puesto que el trayecto de incremento es de longitud como máximo N, cada arco puede tener como máximo N/2, trayectos de incremento, y el número total de trayectos de incremento es como máximo NA/2.
El algoritmo Edmonds-Karp se ejecuta en O(NA^2). Si a lo sumo los caminos NA/2 serán explorados durante el algoritmo y explorar cada trayectoria con BFS es N+A entonces el término más significativo del producto y por lo tanto el complejidad asintótica O(NA^2).
Deja que mfp sea un maxFlowProblemState.
def edmonds_karp(mfp):
sid, tid = mfp.sourceNodeUid, mfp.terminalNodeUid
no_more_paths = False
loop_count = 0
while(not no_more_paths):
residual_digraph = get_residual_graph_of(mfp.G)
try:
asource = find_node_by_uid(mfp.sourceNodeUid, residual_digraph)
aterm = find_node_by_uid(mfp.terminalNodeUid, residual_digraph)
apath = bfs(asource, aterm, residual_digraph)
paint_mfp_path(mfp, loop_count, apath)
G = augment(apath, mfp.G)
s = find_node_by_uid(sid, G)
t = find_node_by_uid(tid, G)
mfp = MaxFlowProblemState(G, s.uid, t.uid, mfp.maxFlowProblemStateUid)
loop_count += 1
except StopIteration as e:
no_more_paths = True
return mfp
La versión anterior es ineficiente y tiene peor complejidad que O(NA^2) ya que construye una nueva solución de flujo máximo y una nueva gráfica residual cada vez (en vez de modificar los dígrafos existentes a medida que avanza el algoritmo). Para llegar a una solución O(NA^2) verdadera el algoritmo debe mantener tanto el digrafo que representa el estado de problema de flujo máximo y su asociado ** gráfico residual. Por tanto, el algoritmo debe evitar repetir innecesariamente **arcos y nodos y actualizar sus valores y valores asociados en el gráfico residual sólo cuando sea necesario.
Para escribir un algoritmo Edmonds Karp más rápido, reescribí varios fragmentos de código de lo anterior. Espero que pasar por el código que generó un nuevo digrafo fue útil en la comprensión de lo que está pasando. En el algoritmo rápido, uso algunos trucos nuevos y estructuras de datos de Python que no quiero detallar. Voy a decir que a.fromNode y a.toNode ahora son tratados como cadenas y uids a nodos. Para este código, deje que mfps sea un maxFlowProblemState
import uuid
def fast_get_mfps_flow(mfps):
flow_from_s = {n for n in mfps.G.setOfNodes if n.uid == mfps.sourceNodeUid}.pop().datum.flowOut
flow_to_t = {n for n in mfps.G.setOfNodes if n.uid == mfps.terminalNodeUid}.pop().datum.flowIn
if( (flow_to_t - flow_from_s) > 0.00):
raise Exception('Infeasible s-t flow')
return flow_to_t
def fast_e_k_preprocess(G):
G = strip_flows(G)
get = dict({})
get['nodes'] = dict({})
get['node_to_node_capacity'] = dict({})
get['node_to_node_flow'] = dict({})
get['arcs'] = dict({})
get['residual_arcs'] = dict({})
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
get['nodes'][a.fromNode.uid] = a.fromNode
get['nodes'][a.toNode.uid] = a.toNode
lark = Arc(a.fromNode.uid, a.toNode.uid, FlowArcDatumWithUid(a.datum.capacity, a.datum.flow, uuid.uuid4()))
if(a.fromNode.uid not in get['arcs']):
get['arcs'][a.fromNode.uid] = dict({a.toNode.uid : dict({lark.datum.uid : lark})})
else:
if(a.toNode.uid not in get['arcs'][a.fromNode.uid]):
get['arcs'][a.fromNode.uid][a.toNode.uid] = dict({lark.datum.uid : lark})
else:
get['arcs'][a.fromNode.uid][a.toNode.uid][lark.datum.uid] = lark
for a in G.setOfArcs:
if a.toNode.uid not in get['arcs']:
get['arcs'][a.toNode.uid] = dict({})
for n in get['nodes']:
get['residual_arcs'][n] = dict()
get['node_to_node_capacity'][n] = dict()
get['node_to_node_flow'][n] = dict()
for u in get['nodes']:
n_to_u_cap_sum = sum(a.datum.capacity for a in G.setOfArcs if (a.fromNode.uid == n) and (a.toNode.uid == u) )
n_to_u_flow_sum = sum(a.datum.flow for a in G.setOfArcs if (a.fromNode.uid == n) and (a.toNode.uid == u) )
if(n_to_u_cap_sum > n_to_u_flow_sum):
flow = round(n_to_u_cap_sum - n_to_u_flow_sum, TOL)
get['residual_arcs'][n][u] = Arc(n,u,ResidualDatum(flow, 'push'))
if(n_to_u_flow_sum > 0.0):
flow = round(n_to_u_flow_sum, TOL)
get['residual_arcs'][u][n] = Arc(u,n,ResidualDatum(flow, 'pull'))
get['node_to_node_capacity'][n][u] = n_to_u_cap_sum
get['node_to_node_flow'][n][u] = n_to_u_flow_sum
return get
def fast_bfs(sid, tid, get):
parent_of = dict([])
visited = frozenset([])
deq = coll.deque([sid])
while len(deq) > 0:
n = deq.popleft()
if n == tid:
break
for u in get['residual_arcs'][n]:
if (u not in visited):
visited = visited.union(frozenset({u}))
parent_of[u] = get['residual_arcs'][n][u]
deq.extend([u])
path = list([])
curr = tid
while(curr != sid):
if (curr not in parent_of):
err_msg = 'No augmenting path from {} to {}.'.format(sid, curr)
raise StopIteration(err_msg)
path.extend([parent_of[curr]])
curr = parent_of[curr].fromNode
path.reverse()
return path
def fast_edmonds_karp(mfps):
sid, tid = mfps.sourceNodeUid, mfps.terminalNodeUid
get = fast_e_k_preprocess(mfps.G)
no_more_paths, loop_count = False, 0
while(not no_more_paths):
try:
apath = fast_bfs(sid, tid, get)
get = fast_augment(apath, get)
loop_count += 1
except StopIteration as e:
no_more_paths = True
nodes = frozenset(get['nodes'].values())
arcs = frozenset({})
for from_node in get['arcs']:
for to_node in get['arcs'][from_node]:
for arc in get['arcs'][from_node][to_node]:
arcs |= frozenset({get['arcs'][from_node][to_node][arc]})
G = DiGraph(nodes, arcs)
mfps = MaxFlowProblemState(G, sourceNodeUid=sid, terminalNodeUid=tid, maxFlowProblemStateUid=mfps.maxFlowProblemStateUid)
return mfps
He aquí una visualización de cómo este algoritmo resuelve el ejemplo red de flujo desde arriba. La visualización muestra los pasos que se reflejan en el digrafo G que representa la red de flujo más actualizada y como se reflejan en el gráfico residual de esa red de flujo . Los caminos de aumento en el gráfico residual se muestran como rutas rojas, y el digrafo que representa el problema el conjunto de nodos y arcos afectados por un dado la ruta de aumento se resalta en verde. En cada caso, resaltaré las partes del gráfico que se cambiarán (en rojo o verde) y luego mostraré el gráfico después de los cambios (sólo en negro).


Aquí hay otra visualización de cómo este algoritmo resolviendo un ejemplo diferente red de flujo. Observe que éste usa números reales y contiene varios arcos con los mismos valores fromNode y toNode.
Observa también que debido a que los Arcos con un ‘pull’ ResidualDatum pueden ser parte de la Vía en Aumento, los nodos afectados en el DíGrafo de la Red de Flujo_no pueden estar en un camino en G!.
Gráficos Bipartitos
Supongamos que tenemos un digrafo G, G es bipartito si es posible particionar los nodos en G.setOfNodes en dos conjuntos (part_1 and part_2) tal que para cualquier arco a en G.setOfArcs no puede ser verdad que a.fromNode en part_1 y a.toNode en part_1. Tampoco puede ser verdad que a.fromNode en part_2 y a.toNode en part_2.
En otras palabras, G es bi-partición si puede dividirse en dos conjuntos de nodos de tal manera que cada arco debe conectar un nodo en un conjunto a un nodo en el otro conjunto.
Pruebas Bipartitas
Supongamos que tenemos un digrafo G, queremos probar si es bi-partición. Podemos hacer esto en O(|G.setOfNodes|+|G.setOfArcs|) por codicioso color de la gráfica en dos colores.
Primero, necesitamos generar un nuevo digrafo H. Este gráfico tendrá tendrá el mismo conjunto de nodos como G, pero tendrá más arcos que G. Cada arco a en G creará 2 arcos en H; el primer arco será idéntico a a, y el segundo arco invierte al director de a ( b = Arc(a.toNode,a.fromNode,a.datum)).
Bipartition = coll.namedtuple('Bipartition',['firstPart', 'secondPart', 'G'])
def bipartition(G):
nodes = frozenset(G.setOfNodes
arcs = frozenset(G.setOfArcs)
arcs = arcs.union( frozenset( {Arc(a.toNode,a.fromNode,a.datum) for a in G.setOfArcs} ) )
H = DiGraph(nodes, arcs)
H_as_dict = digraph_to_dict(H)
color = dict([])
some_node = next(iter(H.setOfNodes))
deq = coll.deque([some_node])
color[some_node] = -1
while len(deq) > 0:
curr = deq.popleft()
for a in H_as_dict.get(curr):
if (a.toNode not in color):
color[a.toNode] = -1*color[curr]
deq.extend([a.toNode])
elif(color[curr] == color[a.toNode]):
print(curr,a.toNode)
raise Exception('Not Bipartite.')
firstPart = frozenset( {n for n in color if color[n] == -1 } )
secondPart = frozenset( {n for n in color if color[n] == 1 } )
if( firstPart.union(secondPart) != G.setOfNodes ):
raise Exception('Not Bipartite.')
return Bipartition(firstPart, secondPart, G)
Coincidencias y Coincidencias Máximas
Supongamos que tenemos un digrafo G y matching es un subconjunto de arcos de G.setOfArcs. matching es un matching si para dos digrafo a y b en matching: len(frozenset( {a.fromNode} ).union( {a.toNode} ).union( {b.fromNode} ).union( {b.toNode} )) == 4. En otras palabras, ningún arco en una coincidencia comparte un nodo.
La coincidencia matching, es una coincidencia máxima si no hay ninguna otra concordancia alt_matching en G tanto que len(matching) < len(alt_matching). En otras palabras, matching es una coincidencia máxima Si es el set más largo de arcos en G.setOfArcs que todavía satisface la definición de combinación (la adición de cualquier arco que no esté ya en la coincidencia romperá la combinación definición).
Una combinación máxima matching es una combinación perfecta si para cada nodo n en G.setOfArcs existe un arco a en matching donde a.fromNode == n or a.toNode == n.
Combinación Bi-Particionada Máxima
Una combinación bi-particionada máxima es una combinación máxima en un digrafo G que es bi-particionado.
Dado que G es bi-particionado, el problema de encontrar una combinación máxima bipartita se puede transformar en un problema de flujo máximo solucionable con el algoritmo de Edmonds-Karp y entonces el acoplamiento bipartito máximo puede ser recuperado del solución al problema de flujo máximo.
Deja que bipartition sea una bi-partición de G.
Para ello, necesito generar un nuevo digrafo (H) con algunos nuevos nodos (H.setOfNodes) y algunos arcos nuevos (H.setOfArcs). H.setOfNodes contiene todos los nodos en G.setOfNodes y dos nodos más, s (un nodo fuente) y t (un nodo terminal).
H.setOfArcs contendrá un arco por cada G.setOfArcs. Si un arco a es un G.setOfArcs y a.fromNode está en bipartition.firstPart y a.toNode está en bipartition.secondPart y luego incluye a en H (agregando un FlowArcDatum(1,0)).
Si a.fromNode es una bipartition.secondPart y a.toNode es una bipartition.firstPart, luego incluye Arc(a.toNode,a.fromNode,FlowArcDatum(1,0)) en H.setOfArcs.
La definición de un gráfico bi-particionado asegura que ningún arco conecte cualquier nodo donde ambos nodos están en la misma partición. H.setOfArcs también contiene un arco de nodo s a cada nodo en bipartition.firstPart. Por último, H.setOfArcs contiene un arco cada node en bipartition.secondPart un nodo t. a.datum.capacity = 1 por todas las a en H.setOfArcs.
Primera partición de los nodos en G.setOfNodes los dos sets (part1 and part2) separados tanto que ningún arco en G.setOfArcs se dirige desde un conjunto al mismo conjunto (esta partición es posible porque G está bi-particionado). A continuación, agregue todos los arcos en G.setOfArcs los cuales están dirigidos de la part1 a la part2 hacia H.setOfArcs. A continuación, cree un único nodo fuente s y un único nodo terminal t y cree más arcos
Luego, construye un maxFlowProblemState.
def solve_mbm( bipartition ):
s = Node(uuid.uuid4(), FlowNodeDatum(0,0))
t = Node(uuid.uuid4(), FlowNodeDatum(0,0))
translate = {}
arcs = frozenset([])
for a in bipartition.G.setOfArcs:
if ( (a.fromNode in bipartition.firstPart) and (a.toNode in bipartition.secondPart) ):
fark = Arc(a.fromNode,a.toNode,FlowArcDatum(1,0))
arcs = arcs.union({fark})
translate[frozenset({a.fromNode.uid,a.toNode.uid})] = a
elif ( (a.toNode in bipartition.firstPart) and (a.fromNode in bipartition.secondPart) ):
bark = Arc(a.toNode,a.fromNode,FlowArcDatum(1,0))
arcs = arcs.union({bark})
translate[frozenset({a.fromNode.uid,a.toNode.uid})] = a
arcs1 = frozenset( {Arc(s,n,FlowArcDatum(1,0)) for n in bipartition.firstPart } )
arcs2 = frozenset( {Arc(n,t,FlowArcDatum(1,0)) for n in bipartition.secondPart } )
arcs = arcs.union(arcs1.union(arcs2))
nodes = frozenset( {Node(n.uid,FlowNodeDatum(0,0)) for n in bipartition.G.setOfNodes} ).union({s}).union({t})
G = DiGraph(nodes, arcs)
mfp = MaxFlowProblemState(G, s.uid, t.uid, 'bipartite')
result = edmonds_karp(mfp)
lookup_set = {a for a in result.G.setOfArcs if (a.datum.flow > 0) and (a.fromNode.uid != s.uid) and (a.toNode.uid != t.uid)}
matching = {translate[frozenset({a.fromNode.uid,a.toNode.uid})] for a in lookup_set}
return matching
Cubierta Mínima de Nodo
Una cubierta de nodo en un dígrafo G es un conjunto de nodos (cover) proveniente de G.setOfNodes tanto que para cualquier arco a de G.setOfArcs esto debe ser verdad: (a.fromNode en cubierta) o (a.toNode en cubierta).
Una cubierta de nodo mínima es el set más pequeño de nodos en la grífica que sigue siendo una cubierta de nodo. El teorema de König indica que en un gráfico bi-particionado, el tamaño de la coincidencia máxima en ese gráfico es igual al tamaño de la cubierta de nodo mínima, y sugiere cómo la cubierta del nodo puede recuperarse de una coincidencia máxima:
Supongamos que tenemos la bi-partición bipartition y la coincidencia máxima matching. Define un nuevo digrafo H, H.setOfNodes=G.setOfNodes, los arcos en H.setOfArcs son la unión de dos sets.
El primer set de arcos a en matching, con el cambio que si a.fromNode in bipartition.firstPart y a.toNode en bipartition.secondPart entonces a.fromNode y a.toNode son intercambiados en el acro creado le dan a tales arcos un atributo a.datum.inMatching = True para indicar que se derivaron de arcos en una coincidencia.
El segundo conjunto es arcos a NO en matching, con el cambio que si a.fromNode en bipartition.secondPart y a.toNode en bipartition.firstPart entonces a.fromNode y a.toNode se intercambian en el arco creado (da a tal arco un atributo a.datum.inMatching = False).
A continuación, ejecute una primera búsqueda de profundidad (DFS) a partir de cada nodo n en bipartition.firstPart que no es n == a.fromNode ni n == a.toNodes para cualquier arco a en matching. Durante el DFS, algunos nodos son visitados y otros no (almacene esta información en un campo n.datum.visited). La cubierta de nodo mínima es la unión de los nodos {a.fromNode para a en H.setOfArcs si ((a.datum.inMatching) y (a.fromNode.datum.visited))} y los nodos {a.fromNode para a en H.setOfArcs si (a.datum.inMatching) y (no a.toNode.datum.visited)}.
Esto puede demostrarse que conduce desde una coincidencia máxima a una cubierta de nodo mínima por una prueba por contradicción, tomar un arco a que supuestamente no estaba cubierto y considerar todos los cuatro casos sobre si a.fromNode y a.toNode pertenecen (ya sea como toNode o fromNode) a cualquier arco en coincidencia matching. Cada caso lleva a una contradicción debido al orden en que DFS visita nodos y el hecho de que matching es un matching máximo.
Supongamos que tenemos una función para ejecutar estos pasos y devolver el conjunto de nodos que comprende la cubierta de nodo mínima cuando se le da el digrafo G, y la coincidencia máxima matching:
ArcMatchingDatum = coll.namedtuple('ArcMatchingDatum', ['inMatching' ])
NodeMatchingDatum = coll.namedtuple('NodeMatchingDatum', ['visited'])
def dfs_helper(snodes, G):
sniter, do_stop = iter(snodes), False
visited, visited_uids = set(), set()
while(not do_stop):
try:
stack = [ next(sniter) ]
while len(stack) > 0:
curr = stack.pop()
if curr.uid not in visited_uids:
visited = visited.union( frozenset( {Node(curr.uid, NodeMatchingDatum(False))} ) )
visited_uids = visited.union(frozenset({curr.uid}))
succ = frozenset({a.toNode for a in G.setOfArcs if a.fromNode == curr})
stack.extend( succ.difference( frozenset(visited) ) )
except StopIteration as e:
stack, do_stop = [], True
return visited
def get_min_node_cover(matching, bipartition):
nodes = frozenset( { Node(n.uid, NodeMatchingDatum(False)) for n in bipartition.G.setOfNodes} )
G = DiGraph(nodes, None)
charcs = frozenset( {a for a in matching if ( (a.fromNode in bipartition.firstPart) and (a.toNode in bipartition.secondPart) )} )
arcs0 = frozenset( { Arc(find_node_by_uid(a.toNode.uid,G), find_node_by_uid(a.fromNode.uid,G), ArcMatchingDatum(True) ) for a in charcs } )
arcs1 = frozenset( { Arc(find_node_by_uid(a.fromNode.uid,G), find_node_by_uid(a.toNode.uid,G), ArcMatchingDatum(True) ) for a in matching.difference(charcs) } )
not_matching = bipartition.G.setOfArcs.difference( matching )
charcs = frozenset( {a for a in not_matching if ( (a.fromNode in bipartition.secondPart) and (a.toNode in bipartition.firstPart) )} )
arcs2 = frozenset( { Arc(find_node_by_uid(a.toNode.uid,G), find_node_by_uid(a.fromNode.uid,G), ArcMatchingDatum(False) ) for a in charcs } )
arcs3 = frozenset( { Arc(find_node_by_uid(a.fromNode.uid,G), find_node_by_uid(a.toNode.uid,G), ArcMatchingDatum(False) ) for a in not_matching.difference(charcs) } )
arcs = arcs0.union(arcs1.union(arcs2.union(arcs3)))
G = DiGraph(nodes, arcs)
bip = Bipartition({find_node_by_uid(n.uid,G) for n in bipartition.firstPart},{find_node_by_uid(n.uid,G) for n in bipartition.secondPart},G)
match_from_nodes = frozenset({find_node_by_uid(a.fromNode.uid,G) for a in matching})
match_to_nodes = frozenset({find_node_by_uid(a.toNode.uid,G) for a in matching})
snodes = bip.firstPart.difference(match_from_nodes).difference(match_to_nodes)
visited_nodes = dfs_helper(snodes, bip.G)
not_visited_nodes = bip.G.setOfNodes.difference(visited_nodes)
H = DiGraph(visited_nodes.union(not_visited_nodes), arcs)
cover1 = frozenset( {a.fromNode for a in H.setOfArcs if ( (a.datum.inMatching) and (a.fromNode.datum.visited) ) } )
cover2 = frozenset( {a.fromNode for a in H.setOfArcs if ( (a.datum.inMatching) and (not a.toNode.datum.visited) ) } )
min_cover_nodes = cover1.union(cover2)
true_min_cover_nodes = frozenset({find_node_by_uid(n.uid, bipartition.G) for n in min_cover_nodes})
return min_cover_nodes
El Problema de Asignación Lineal
El problema de asignación lineal consiste en encontrar una máxima coincidencia de pesos en un gráfico bipartito ponderado.
Problemas como el que aparece al comienzo de este post pueden expresarse como un problema de asignación lineal. Dado un conjunto de trabajadores, un conjunto de tareas, y una función que indica la rentabilidad de una asignación de un trabajador a una tarea, queremos maximizar la suma de todas las asignaciones que hacemos; esto es un problema de asignación lineal.
Supongamos que el número de tareas y los trabajadores son iguales, aunque voy a demostrar que esta suposición es fácil de quitar. En la implementación, represento pesos de arco con un atributo a.datum.weight para un arco a.
WeightArcDatum = namedtuple('WeightArcDatum', [weight])
Algoritmo Kuhn-Munkres
El Algoritmo de Kuhn-Munkres resuelve el problema de asignación lineal. Una buena implementación puede tomar tiempo O(N^{4}),
(donde N es el número de nodos en el digrafo que representa el problema). Una implementación que es más fácil de explicar toma O (N ^ {5}) (para una versión que regenera digrafos) y O (N ^ {4}) para (para una versión que mantiene los digrafos). Esto es similar a las dos implementaciones diferentes del algoritmo Edmonds-Karp.
Para esta descripción, sólo estoy trabajando con gráficos bipartitos completos (aquellos donde la mitad de los nodos están en una parte de la bi-partición y la otra mitad en la segunda parte). En el trabajador, la motivación de la tarea significa que hay tantos trabajadores como tareas.
Esto parece una condición significativa (¿qué sucede si estos conjuntos no son iguales?), Pero es fácil solucionar este problema; Hablo de cómo hacerlo en la última sección.
La versión del algoritmo descrito aquí utiliza el concepto útil de arcos de peso cero. Desafortunadamente, este concepto sólo tiene sentido cuando estamos resolviendo una minimización (si en vez de maximizar los beneficios de nuestras asignaciones de tareas de trabajadores, en vez de eso minimizamos el costo de tales asignaciones).
Afortunadamente, es fácil convertir un problema de asignación lineal máximo en un problema de asignación lineal mínimo estableciendo cada uno de los pesos de arco a en M-a.datum.weight donde M=max({a.datum.weight for a in G.setOfArcs}).
La solución al problema de maximización original será idéntica a la solución minimizando el problema después de que se cambien los pesos de arco. Así que para el resto, supongamos que hacemos este cambio.
El algoritmo Kuhn-Munkres resuelve
ponderación de peso mínima en un gráfico bi-particionado ponderado por una secuencia de concordancias máximas en gráficos no ponderados bipartitos. Si a encontramos una concordancia perfecta en la representación del digrafo del problema de asignación lineal y si el peso de cada arco en la coincidencia es cero, entonces hemos encontrado la ponderación de peso mínimo ya que esta coincidencia sugiere que todos nodos en el digrafos han sido emparejado por un arco con el menor costo posible ( ningún coste puede ser inferior a 0, basado en definiciones anteriores).
Ningún otro arcos se puede agregar a la coincidencia (ya que todos nodos ya están emparejados) y no arcos debe ser eliminado de la coincidente porque cualquier posible reemplazo arco tendrá al menos un valor de peso tan grande.
Si encontramos una coincidencia máxima del subgrafo
de G que contiene sólo arcos de peso cero, y no es una concordancia perfecta, no tenemos una solución completa (ya que la combinación no es perfecta). Sin embargo, podemos producir un nuevo digrafo H cambiando los pesos de arcos en G.setOfArcs de manera que aparezcan nuevos 0-peso arcos y la solución óptima de «H» es la misma que la solución óptima de «G». Dado que garantizamos que al menos un arco de peso cero se produce en cada iteración, garantizamos que llegaremos a un coincidencia perfecta en no más de |G.setOfNodes|^{2}=N^{2} en tales iteraciones.
Supongamos que en la bi-partición bipartition, bipartition.firstPart contiene nodos representando trabajadores, y bipartition.secondPart representa nodos que al mismo tiempo representa pruebas.
El algoritmo comienza generando un nuevo digrafo H. H.setOfNodes = G.setOfNodes. Algunos arcos en H son nodos n generados en bipartition.firstPart. Cada nodo n genera un arco b en H.setOfArcs por cada arco a en bipartition.G.setOfArcs donde a.fromNode = n or a.toNode = n, b=Arc(a.fromNode, a.toNode, a.datum.weight - z) donde z=min(x.datum.weight for x in G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )).
Más arcos en H se generan por nodos n en bipartition.secondPart. Cada uno de estos nodos n genera un arco b en H.setOfArcs por cada arco a en bipartition.G.setOfArcs donde a.fromNode = n o a.toNode = n, b=Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) donde z=min(x.datum.weight for x in G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )).
KMA: Luego, forma un nuevo digrafo K compuesto sólo de los arcos de peso cero de H, y los nodos incidente
en esos arcos. Forma una bipartition en los nodos en K, luego usa solve_mbm( bipartition ) para obtener una combinación máxima (matching) en K. Si matching es una combinación perfecta en H (los arcos en matching son incidente en todos los nodos en H.setOfNodes) entonces matching es una solución óptima para problema de asignación lineal.
De lo contrario, si matching no es perfecto, genera la cubierta de nodo mínima de K usando node_cover = get_min_node_cover(matching, bipartition(K)). Luego, define z=min({a.datum.weight for a in H.setOfArcs if a not in node_cover}). Define nodes = H.setOfNodes, arcs1 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh-z)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) and (a.toNode not in node_cover)}, arcs2 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) != (a.toNode not in node_cover)}, arcs3 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh+z)) for a in H.setOfArcs if ( (a.fromNode in node_cover) and (a.toNode in node_cover)}. El != símbolo en la expresión anterior actúa como un operador XOR. Luego arcs = arcs1.union(arcs2.union(arcs3)). Luego, H=DiGraph(nodes,arcs). Regresa a la marca KMA. El algoritmo continúa hasta que se produce una combinación perfecta. Esta combinación es también la solución al problema de asignación lineal.
def kuhn_munkres( bipartition ):
nodes = bipartition.G.setOfNodes
arcs = frozenset({})
for n in bipartition.firstPart:
z = min( {x.datum.weight for x in bipartition.G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )} )
arcs = arcs.union( frozenset({Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) }) )
for n in bipartition.secondPart:
z = min( {x.datum.weight for x in bipartition.G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )} )
arcs = arcs.union( frozenset({Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) }) )
H = DiGraph(nodes, arcs)
assignment, value = dict({}), 0
not_done = True
while( not_done ):
zwarcs = frozenset( {a for a in H.setOfArcs if a.datum.weight == 0} )
znodes = frozenset( {n.fromNode for n in zwarcs} ).union( frozenset( {n.toNode for n in zwarcs} ) )
K = DiGraph(znodes, zwarcs)
k_bipartition = bipartition(K)
matching = solve_mbm( k_bipartition )
mnodes = frozenset({a.fromNode for a in matching}).union(frozenset({a.toNode for a in matching}))
if( len(mnodes) == len(H.setOfNodes) ):
for a in matching:
assignment[ a.fromNode.uid ] = a.toNode.uid
value = sum({a.datum.weight for a in matching})
not_done = False
else:
node_cover = get_min_node_cover(matching, bipartition(K))
z = min( frozenset( {a.datum.weight for a in H.setOfArcs if a not in node_cover} ) )
nodes = H.setOfNodes
arcs1 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh-z)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) and (a.toNode not in node_cover)} )
arcs2 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) != (a.toNode not in node_cover)} )
arcs3 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh+z)) for a in H.setOfArcs if ( (a.fromNode in node_cover) and (a.toNode in node_cover)} )
arcs = arcs1.union(arcs2.union(arcs3))
H = DiGraph(nodes,arcs)
return value, assignment
Esta implementación es O(N^{5}) porque genera una nueva combinación máxima matching en cada iteración; similar a las dos implementaciones anteriores de Edmonds-Karp este algoritmo puede ser modificado para que siga la pista de la coincidencia y la adapte inteligentemente a cada iteración. Cuando esto se hace, la complejidad se convierte en O(N^{4}). Una versión más avanzada y más reciente de este algoritmo (que requiere algunas estructuras de datos más avanzadas) puede ejecutarse en O (N ^ {3}). Detalles de la implementación más sencilla anterior y la implementación más avanzada se puede encontrar en esta publicación que motivó este blog.
Ninguna de las operaciones sobre los pesos del arco modifica la asignación final devuelta por el algoritmo. Por eso: Dado que nuestros gráficos de entrada son siempre gráficos completos bi-particionados, una solución debe asignar cada nodo en una partición a otro nodo en la segunda partición, a través del arco entre estos dos nodos. Observe que las operaciones realizadas en los pesos de arco nunca cambian el orden (ordenado por peso) de los arcos incidentes en ningún nodo particular.
Por lo tanto, cuando el algoritmo termina en un perfecta y completa bi-partición coincidente, cada nodo se le asigna un peso cero al arco, ya que el orden relativo de los arcos de que nodo no ha cambiado durante el algoritmo y dado que un arco de peso cero es el arco más barato posible y el complemento bipartito completo perfecto garantiza que existe un arco para cada nodo. Esto significa que la solución generada es de hecho la misma que la solución del problema de asignación lineal original sin ninguna modificación de pesos de arco.
Asignaciones no Balanceadas
Parece que el algoritmo es bastante limitado, ya que como se describe, opera sólo en gráficos bipartitos completos (aquellos donde la mitad de los nodos están en una parte de la bi-partición y la otra mitad en el segundo parte). En el trabajador, la motivación de la tarea significa que hay tantos trabajadores como tareas (parece bastante limitante).
Sin embargo, hay una transformación fácil que elimina esta restricción. Supongamos que hay menos trabajadores que tareas, agregamos algunos trabajadores ficticios (lo suficiente para hacer que el gráfico resultante sea un gráfico bipartito completo). Cada trabajador ficticio tiene un arco dirigido del trabajador a cada una de las tareas. Cada uno de estos arco tiene peso 0 (colocándolo en una coincidencia no da ningún beneficio adicional). Después de este cambio el gráfico es un gráfico bipartito completo que podemos resolver. No se inicia ninguna tarea asignada a un trabajador ficticio.
Supongamos que hay más tareas que los trabajadores. Añadimos algunas tareas ficticias (suficiente para hacer que el gráfico resultante sea un gráfico bi-particionado completo). Cada tarea ficticia tiene un arco dirigido de cada trabajador a la tarea ficticia. Cada uno de estos arco tiene un peso de 0 (colocándolo en una coincidencia no da ningún beneficio adicional). Después de este cambio el gráfico es un gráfico bi-particionado completo que podemos resolver. Cualquier trabajador asignado a la tarea ficticia no es empleado durante el período.
Ejemplo de asignación lineal
Por último, vamos a hacer un ejemplo con el código que he estado usando. Voy a modificar el ejemplo de problema de aquí. Tenemos 3 tareas: necesitamos limpiar el baño, barrer el piso, y lavar las ventanas.
Los trabajadores disponibles son Alice, Bob, Charlie y Diane. Cada uno de los trabajadores nos da el salario que requieren por tarea. Aquí están los salarios por trabajador:
|
Clean the Bathroom |
Sweep the Floor |
Wash the Windows |
| Alice |
$2 |
$3 |
$3 |
| Bob |
$3 |
$2 |
$3 |
| Charlie |
$3 |
$3 |
$2 |
| Diane |
$9 |
$9 |
$1 |
Si queremos pagar la menor cantidad de dinero, pero todavía obtener todas las tareas realizadas, ¿quién debe hacer qué tarea? Comienza introduciendo una tarea ficticia para que el digrafo que representa el problema bipartito.
|
Clean the Bathroom |
Sweep the Floor |
Wash the Windows |
Do Nothing |
| Alice |
$2 |
$3 |
$3 |
$0 |
| Bob |
$3 |
$2 |
$3 |
$0 |
| Charlie |
$3 |
$3 |
$2 |
$0 |
| Diane |
$9 |
$9 |
$1 |
$0 |
Suponiendo que el problema está codificado en un digrafo, entonces kuhn_munkres( bipartition(G) ) resolverá el problema y devolverá la asignación. Es fácil verificar que la asignación óptima (costo más bajo) costará $ 5.
He aquí una visualización de la solución que el código anterior genera:


Eso es todo . Ya sabes todo lo que necesitas saber sobre el problema de asignación lineal.
Puedes encontrar todo el código de este artículo en GitHub.
Por: Dmitri Ivanovich Arkhipov
Artículo vía: Toptal